Merasionalkan akar biasanya dipakai ke dalam bilangan berakar yang dalam bentuk pecahan
ingat bahwa (a-b)=a^2-b^2) maka berlaku pula pada bentuk akar sehingga :
maka berlaku pula pada bentuk akar sehingga :
Beginilah caranya :
A. Bentuk 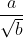
Untuk merasionalkan penyebut bentuk akar 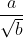 maka kita kalikan dengan penyebut bentuk akar tersebut ( kalikan dengan
maka kita kalikan dengan penyebut bentuk akar tersebut ( kalikan dengan 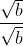 )
)
Contoh soal :
B. Bentuk 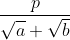 atau
atau 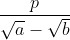
Untuk merasionalkan penyebut bentuk akar seperti ini maka kita kalikan dengan sekawan penyebut bentuk akar tersebut.
Sekawan dari 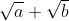 adalah
adalah 
Sekawan dari 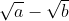 adalah
adalah 
* ingat \left&space;({{\color{Red}&space;\sqrt{a}-\sqrt{b}}}&space;\right&space;)={\color{Red}&space;a-b})
Tidak ada komentar:
Posting Komentar